Edukacja 
Ekologia 
Energetyka 
Fact-checking 
Klimat 
Rosja 
UE 
Ukraina 
Wybory 
Skopiuj link
Drukuj
Udostępnij
16 min czytania
Opisujemy ważne dla debaty publicznej tematy dotyczące polityki, fact-checkingu, dezinformacji i propagandy.
16 min czytania
Dane na wykresach – trzy typowe błędy i jak je rozpoznać
Jak nie dać się wprowadzić w błąd przez źle wykonany wykres? W tym tekście znajdziesz praktyczne wskazówki!
Jak nie dać się wprowadzić w błąd przez źle wykonany wykres? W tym tekście znajdziesz praktyczne wskazówki!
Mawia się, że jeden obraz wart jest tyle co tysiąc słów. Rzeczywiście, nawet skomplikowane dane przedstawione w sposób graficzny mogą sprawiać wrażenie bardziej przystępnych i zrozumiałych. Ale co, jeśli ta graficzna prezentacja wprowadza w błąd? Zdarza się tak, że pierwotne informacje są poprawne, ale przedstawiono je w nieprawidłowy sposób.
Taki przykład znajdziesz na grafice opublikowanej w styczniu br. na Twitterze na profilu Instytutu Badań Rynkowych i Społecznych IBRIS. Przedstawia ona poparcie dla poszczególnych partii politycznych w postaci wykresu, na którym zamiast słupków pokazano głowy liderów ugrupowań.
Fot. Twitter
O takim wykresie można powiedzieć wiele, ale przede wszystkim zwróć uwagę na wielkość poparcia dla Polski 2050 (głowa Szymona Hołowni) oraz dla Koalicji Obywatelskiej (głowa Donalda Tuska). Poparcie dla Polski 2050 wynosi 9,2 proc., a dla KO – prawie 3 razy więcej, bo 25,4 proc. Czy poprawnie odzwierciedlono te wartości rozmiarem głów na wykresie?
W obecnym układzie wydaje się, że poparcie dla kolejnych kandydatów spada stopniowo, podczas gdy liczby wskazują na inną sytuację – głowa Hołowni powinna być prawie trzy razy mniejsza od głowy Tuska, gdyby głowy odzwierciedlały faktyczne wyniki. Tymczasem na tej rycinie głowa lidera Polski 2050 sięga konkurentowi powyżej ucha. Ten przykład może się wydawać komiczny… ale ilustruje, w jaki sposób niepoprawną wizualizacją danych można – celowo lub całkiem przypadkiem – wprowadzić odbiorców w błąd.
W tej analizie znajdziesz więcej takich przykładów, uporządkowanych z uwzględnieniem trzech typowych nieprawidłowości, które pojawiają się na wykresach, potencjalnie wprowadzając internautów w błąd. Na końcu tekstu znajdziesz listę błędów, które – znalezione na wykresie – powinny wzbudzić twoją czujność i skłonić do głębszej weryfikacji zaprezentowanych danych.
Błąd 1: elastyczna statystyka, czyli porównywanie nieporównywalnego
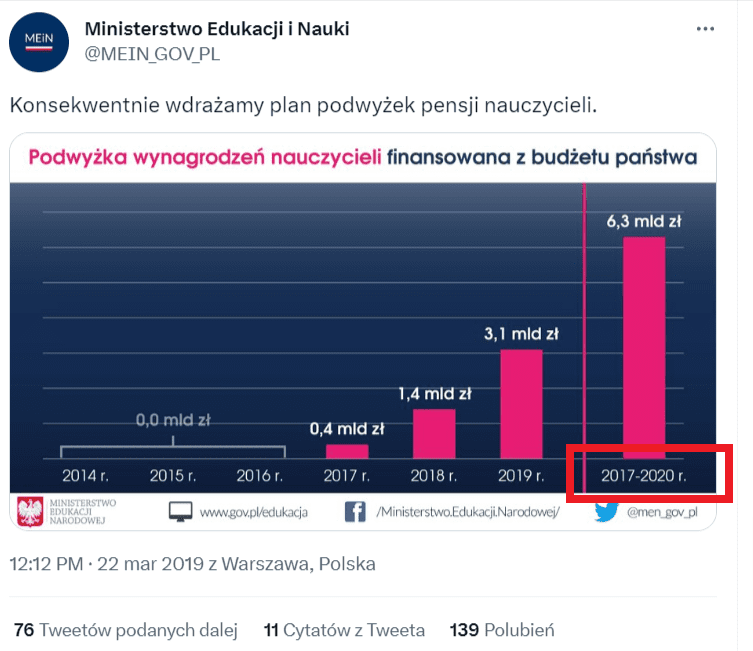
Wykresy pomagają przetwarzać dane, ponieważ przedstawiają je w przystępnej, graficznej formie, przez co łatwiej jest szybko dojść do najważniejszych wniosków. Problem pojawia się wtedy, gdy stoisz przed zadaniem przeanalizowania danych, które pochodzą z nierównych zbiorów. Przykładu dostarczyło Ministerstwo Edukacji i Nauki, które w 2019 roku, w czasie gdy nastroje związane z pensjami nauczycieli były bardzo burzliwe, opublikowało na swoim koncie na Twitterze taki wykres:
Fot. Twitter
Wykres ma przedstawiać wysokość podwyżek dla nauczycieli, finansowanych z budżetu państwa w kolejnych latach. Jeśli spojrzysz na grafikę pobieżnie, szybko dojdziesz do wniosku, że podwyżki rosną z każdym rokiem, a największe są w ostatnim analizowanym okresie. Tylko jaki jest to okres?
Zsumowane lata: nie należy porównywać jednego roku do kilkuletniego okresu
Pierwsze słupki od lewej strony ilustrują podwyżki finansowane w latach: 2014, 2015, 2016, 2017, 2018 i 2019. A co się stało z ostatnim słupkiem, widocznym skrajnie po prawej stronie? Otóż przedstawia on sumaryczną wysokość podwyżek w latach 2017–2020. To aż 4 lata podwyżek zaprezentowanych na jednym słupku.
Nie można porównywać ze sobą danych z jednego roku z danymi zsumowanymi z 4 lat. W zakresie danych z lat 2017–2020 mieszczą się już dane przedstawione na wcześniejszych słupkach dla lat: 2017, 2018 i 2019 – po co je ponownie przedstawiać? Co więcej, wykres opublikowano w 2019 roku, więc dane dotyczące kolejnego – 2020 roku – są jedynie deklaratywne, bo dotyczą przyszłych działań.
Na powyższym wykresie nie zadbano też o czytelne oznaczenie osi Y, ale przynajmniej można wnioskować, że zaczyna się ona prawidłowo: od wartości 0 (zero). To oznacza, że wysokości słupków najpewniej odpowiadają w realny sposób wartościom liczbowym, które reprezentują.
Chwytliwy tytuł – czyli znajdź na wykresie to, czego chciał autor
Na powyższym przykładzie pokazaliśmy, jak wygląda nieprawidłowe porównywanie wartości jednostkowych (1 rok) i zbiorczych (kilka lat). Czasami nieprawidłowość wykresu polega jednak na tym, że ich autorzy zestawiają ze sobą dane, których nie da się poprawnie porównać, np. grupy danych o odmiennym składzie i liczebności.
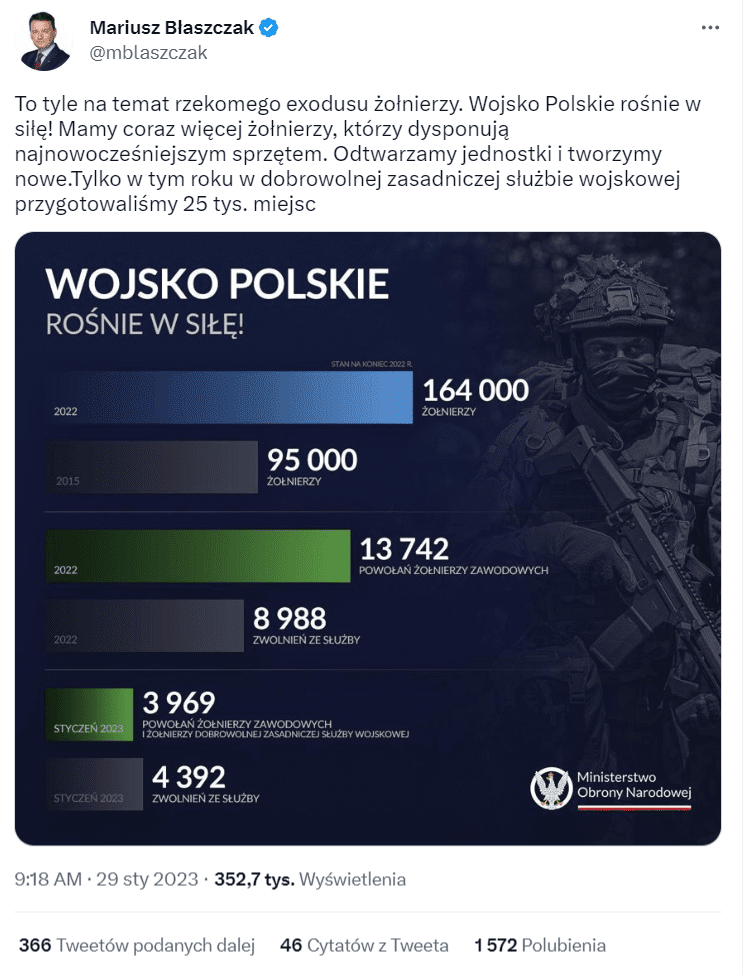
Dobrym przykładem jest wykres udostępniony przez Mariusza Błaszczaka, ministra obrony narodowej:
Fot. Twitter
Już sam tytuł wykresu jest bardzo nieprecyzyjny i sprawia wrażenie pisania pod z góry założoną tezę, którą mamy odnaleźć na grafice, a nie – wyczytać z danych. Tytuł brzmi: „Wojsko Polskie rośnie w siłę!” (teza), a zgodnie ze sztuką tworzenia wykresu powinien opisywać, jakie dane zaprezentowano na grafice, np. „porównanie liczby powołań z liczbą zwolnień ze służby” (opis). To jednak niejedyny i wcale nie największy problem tego wykresu.
„Mgła” na wykresie i nierówne skale
Drugi problem to sposób przedstawienia danych. Czytelność to jedna z najważniejszych cech dobrze wykonanego wykresu. Tymczasem tutaj nie widać osi X i Y, a baza słupków „znika we mgle”, przez co trudno jest wyznaczyć ich precyzyjny początek. Nie podpisano też skali ani wartości 0 (zero) – wszystko to znacząco wpływa na czytelność.
Fot. Twitter
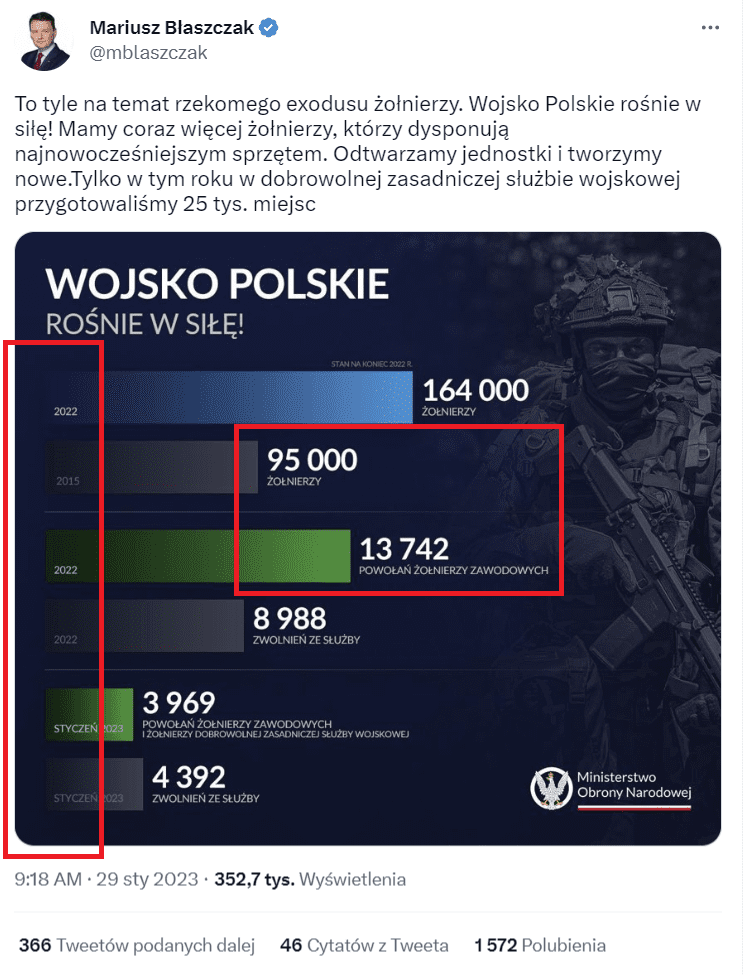
Co więcej, zestawiono ze sobą trzy odrębne grupy danych, przez co skala ulega zaburzeniu. Zwróć uwagę, że słupek podpisany: „13 742 powołań żołnierzy zawodowych” jest wyższy niż znajdujący się tuż nad nim – o opisie: „95 000 żołnierzy”. To sprawia wrażenie, jakby w 2022 roku więcej żołnierzy zostało powołanych do służby, niż w 2015 roku było ich łącznie w całej armii.
Porównywanie nieporównywalnych danych
Trzecia kwestia dotyczy samych danych przedstawionych na wykresie. Grafika zestawia wartości, których nie da się poprawnie porównać, np. w części wykresu poświęconej sumarycznej liczbie żołnierzy (dwa najwyższe słupki) porównano ze sobą dwie odmienne grupy danych.
Do słupka reprezentującego 2015 rok włączono tylko żołnierzy zawodowych, których było wtedy 95 tys. (1, 2, 3). Natomiast do tego, który przedstawia stan wojska w 2022 roku, wliczono żołnierzy zawodowych oraz wielu innych, m.in. studentów szkół wojskowych, którzy ukończyli pierwszy rok, oraz np. terytorialsów (Wojska Obrony Terytorialnej), których w 2015 roku jeszcze w ogóle nie było.
Fot. Twitter
Błąd 2: klasyka gatunku złych wykresów, czyli zagubiona oś Y
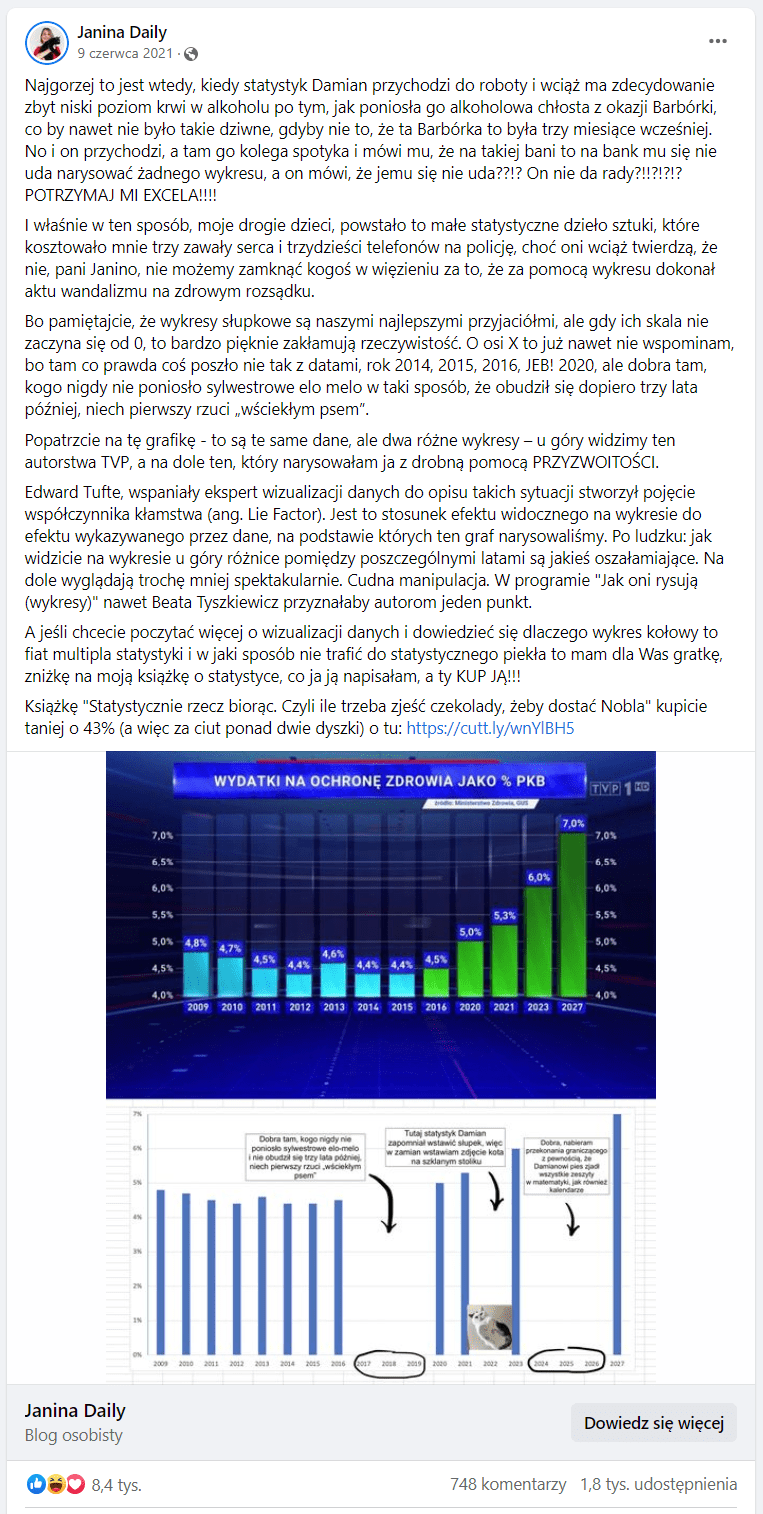
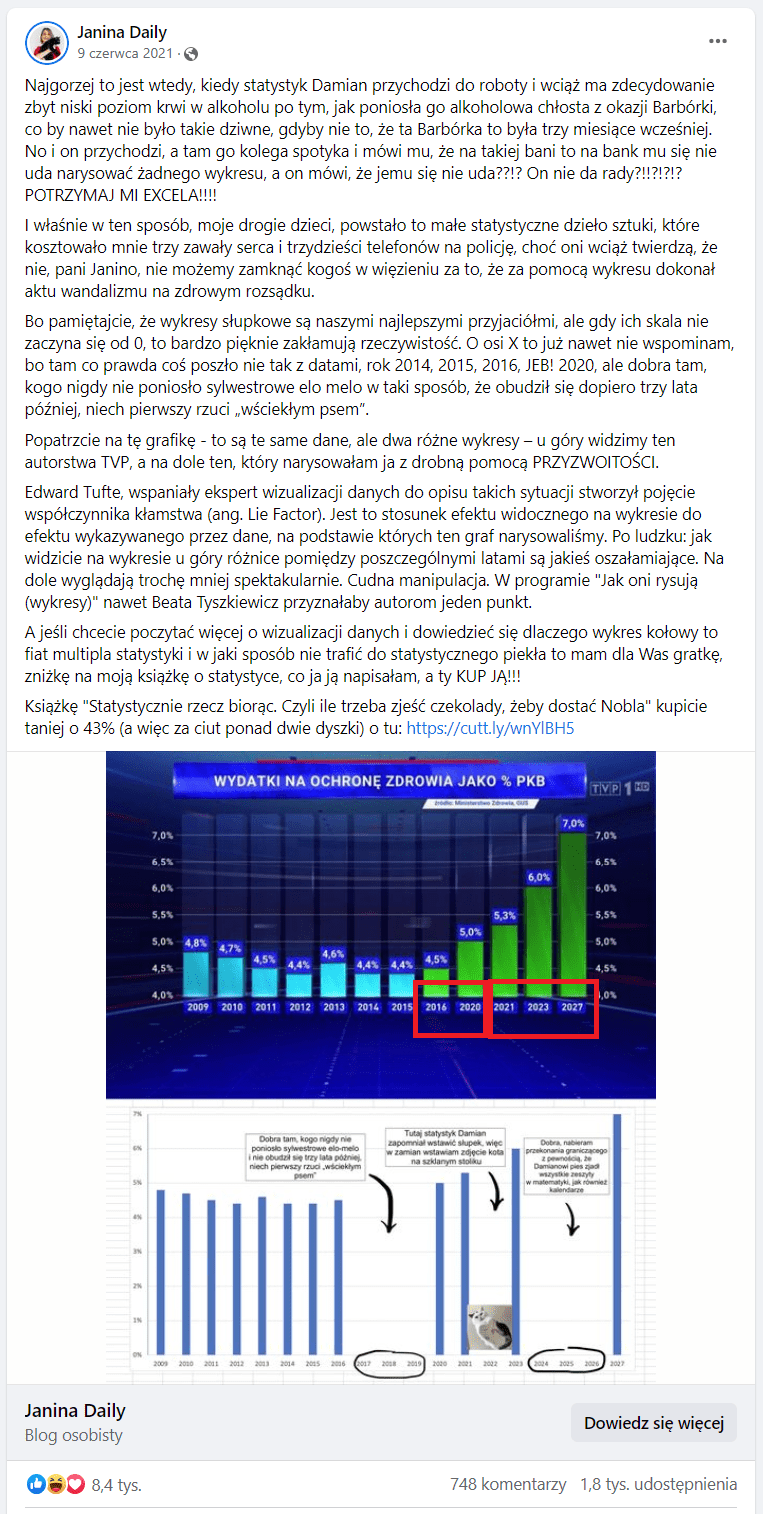
Jednymi z najczęstszych problemów z nierzetelnymi wykresami są: brak odpowiedniego opisu na osi Y, niezachowana skala na tej osi lub rozpoczynanie jej od wartości innej niż 0 (zero). Zobaczmy, na czym polega problem na przykładzie kultowego już (1, 2, 3) wykresu wyemitowanego w 2021 roku przez Telewizję Polską. Pisała o nim m.in. Janina Bąk, statystyczka i popularyzatorka nauki, na swoim profilu na Facebooku.
Fot. Facebook
Zaprezentowana grafika ma przedstawiać wysokość wydatków na ochronę zdrowia jako odsetek PKB. Pierwsze, co zwraca uwagę, jest oś Y. Nie zaczyna się ona – tak jak powinna – od wartości 0, lecz od 4 proc.
Powoduje to, że różnice pomiędzy wysokością poszczególnych słupków są wizualnie bardziej wyolbrzymione. W kontekście danych sprawia to wrażenie znacznie większego wzrostu wartości, niż jest on w rzeczywistości, a przecież różnica pomiędzy najniższą daną (4,4 proc.) a najwyższą (7 proc.) na tym wykresie wynosi relatywnie niedużo, bo 2,6 punktów proc.
Zagubione lata na wykresie
Drugi problem leży w osi X. Gdy podążamy wzrokiem od lewej strony wykresu, zauważamy, że na początku słupki przedstawiają dane w zestawieniu rocznym: 2009, 2010, 2011 i tak dalej, a potem ten układ się zmienia: pomiędzy rokiem 2016 a 2020 pozostawiono lukę w danych – następuje przeskok o kilka lat.
Fot. Facebook
To sprawia wrażenie znacznie większego kontrastu: tak, jakby po 2016 roku doszło do nagłej zmiany w wydatkach na ochronę zdrowia, dzięki czemu uwypukla się dokonania rządu. W dodatku wygląda to tak, jakby ta zmiana objawiała się w bardzo dynamicznym wzroście nakładów finansowych po długim okresie zastoju.
Powrót do przyszłości
Kolejna kwestia dotyczy dwóch ostatnich słupków po prawej stronie wykresu. Przedstawiają one dane za rok 2023 oraz 2027, tyle że emisja programu, w którym przedstawiono ten wykres, nastąpiła w roku 2021. Wynika z tego, że te informacje były wówczas jedynie deklaratywne, co sprawia, że porównano dane teraźniejsze – faktyczne z danymi intencyjnymi – przyszłymi, których nie da się w chwili publikacji potwierdzić.
Manipulacja kolorami
Wątpliwości budzi kolorystyka wykresu. Słupki umieszczone po lewej stronie mają jasnoniebieski kolor, a te po prawej stronie – zaczynając od 2016 roku – jasnozielony kolor.
Ten drugi kolor mocno się wybija, co dodatkowo wzmacnia wrażenie, że w 2016 roku nastąpiła jakaś nagła, pozytywna zmiana, po której wartości liczbowe zaczęły być coraz „lepsze”. Jednak gdy przyjrzymy się wykresowi dokładniej, to zauważymy, że zielony słupek z 2016 roku jest tak naprawdę niższy niż błękitne słupki z lat 2009, 2010, 2011 i 2013.
Jak bardzo przepłacisz za lot?
Problemy z „zagubioną” osią Y zdarzają się oczywiście nie tylko w grafikach przygotowywanych przez podmioty rządowe czy medialne, ale też na wykresach udostępnianych przez podmioty komercyjne. W takim przypadku odbiorcą wykresu jest konsument, który powinien móc zaufać udostępnionym mu danym, bo przecież bardzo możliwe, że na ich podstawie podejmie decyzję dotyczącą zakupu.
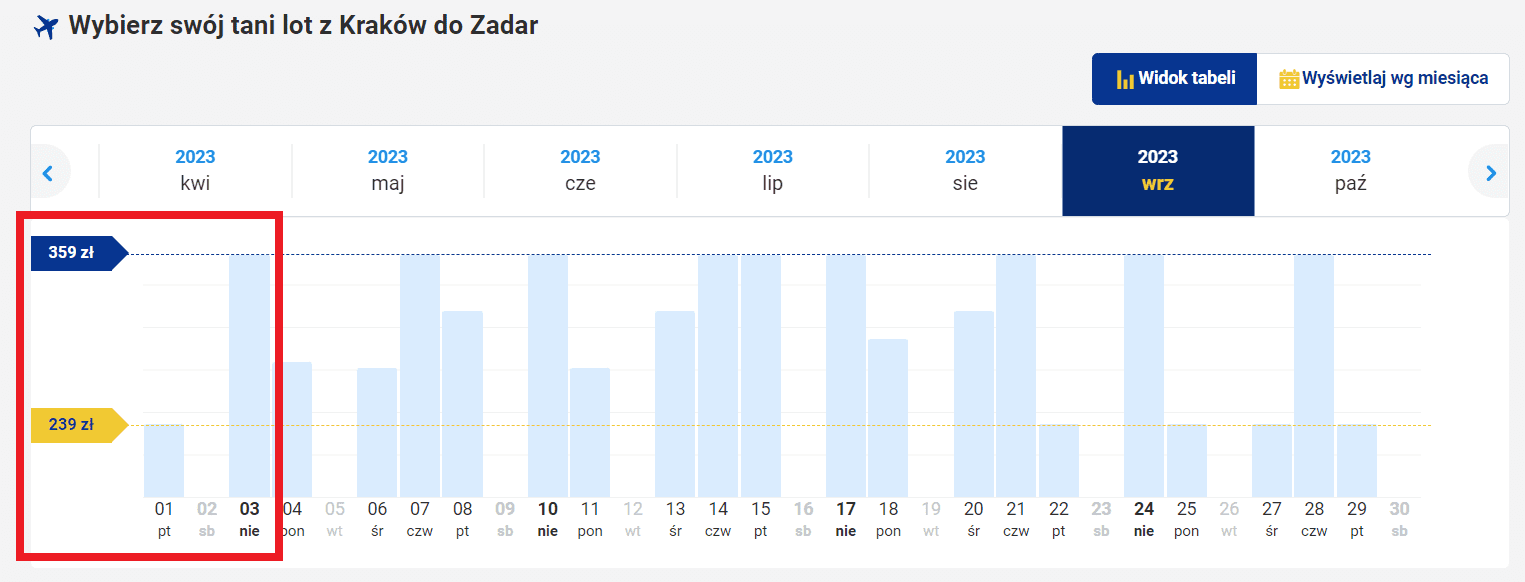
Dobrym przykładem są w tym przypadku wyszukiwarki lotów pasażerskich. Przyjmijmy, że jesienią 2023 roku planujesz lecieć z Krakowa do Zadaru (Chorwacja). Wpisujesz odpowiednie dane w wyszukiwarkę lotów (tu: Ryanair), strona zwraca ci następujące wyniki:
Fot. www.ryanair.pl
Ile razy droższy bilet?
Jak widać na wykresie, we wrześniu ceny są dość zróżnicowane. Najtańszy lot kosztuje 239 zł, a najdroższy 359 zł. Z pozoru wszystko wygląda rzetelnie: oznaczono daty oraz zakres cen, a słupki wizualizują dane. Widać od razu, że bilet za 359 zł jest dużo droższy od biletu za 239 zł… Ale w zasadzie – ile razy droższy jest ten pierwszy?
Jeśli spojrzysz na słupek przy dacie 1 września i porównasz go ze słupkiem obok (z 3 września), zobaczysz, że ten drugi jest ponad trzy razy wyższy od tego pierwszego. Wydawałoby się więc, że cena biletu również jest trzykrotnie większa, prawda? Ale zaraz… 239 zł x 3 = 717 zł, co oznacza, że gdyby ten wykres został prawidłowo wykonany, to wyższy słupek ilustrowałby cenę wynoszącą ponad 700 zł, a nie – jak teraz – cenę 359 zł.
Kiedy różnica pomiędzy słupkami jest tak nieprawidłowo wyolbrzymiona, możesz odnieść wrażenie, że różnica cen również jest znacznie większa niż w rzeczywistości. Gdyby ten wykres został wykonany prawidłowo, słupki rozpoczynałyby się od ceny 0 (zera) zł i wtedy porównanie ich wysokości poprawnie odzwierciedlałoby różnicę cen poszczególnych lotów.
Przesadne proporcje na wykresie
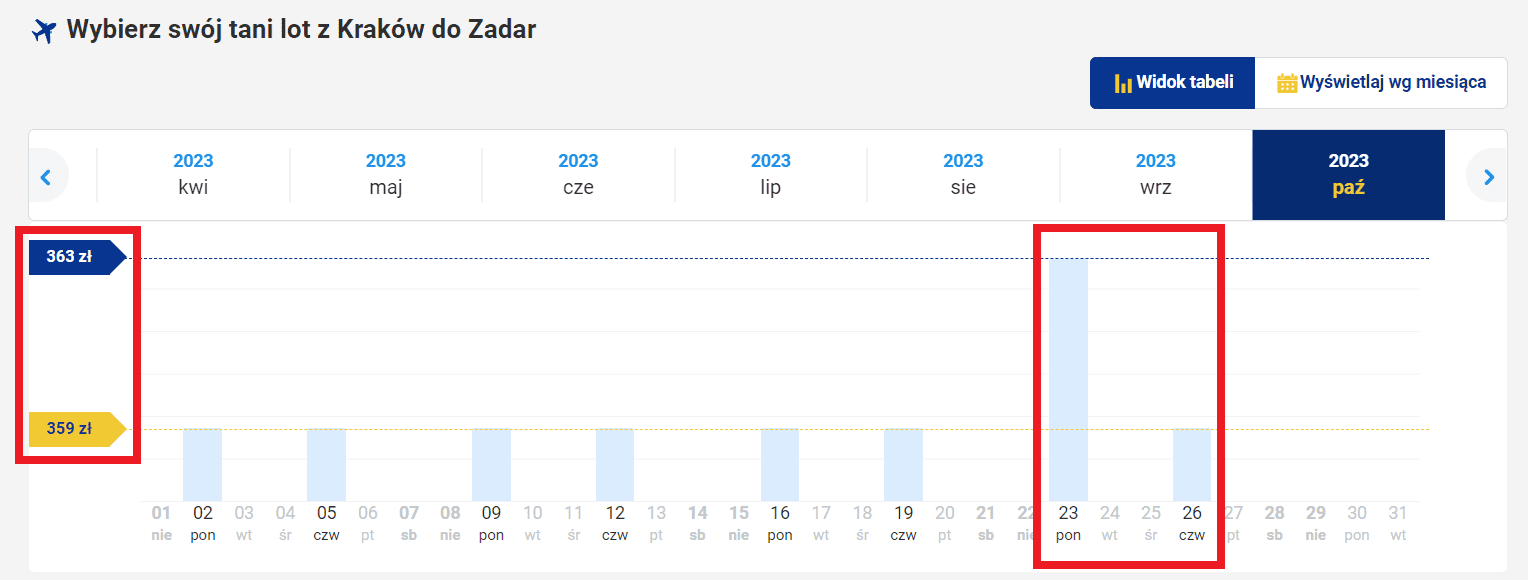
Każdy potencjalny pasażer powinien po prostu przeczytać kwotę widniejącą przy danym locie, jednak nie zmienia to faktu, że gdy patrzymy na tak ułożony wykres, możemy ulec mylnemu wrażeniu. Niestety musimy na to uważać. Stosunki wielkości słupków są jeszcze bardziej przesadne, gdy wybierze się inny zakres dat, np. październik 2023 roku:
Fot. www.ryanair.pl
Tutaj dane są przedstawione w jeszcze mniej rzetelny sposób: najniższa cena lotu to 359 zł, a najwyższa – 363 zł. Różnica tych kwot wynosi zaledwie 4 zł, podczas gdy słupki wykresu sugerują, że pasażer, który zdecyduje się lecieć 23 października, zapłaci ponad trzykrotnie wyższą cenę, niż gdyby zdecydował się na inny termin w tym samym miesiącu. Takie zabiegi wprowadzają w błąd, nawet jeśli nie prezentują mylnych wartości liczbowych, a „jedynie” źle przedstawiają je graficznie.
Błąd 3: chaos w prezentacji danych lub niedobór danych
W jednym z poprzednich przykładów przytoczyliśmy nieprawidłowości na wykresie przygotowanym przez TVP. Oczywiście, nie jest to jedyne medium, które popełnia tego typu błędy. W maju 2020 roku w Faktach TVN opublikowano (podstrona została już usunięta) wykres liniowy, który miał ukazywać, w jaki sposób zmienia się liczba aktywnych zakażeń koronawirusem w wybranych krajach od 15 lutego do 17 maja 2020 roku. Tym razem TVP Info postanowiło omówić ten wykres na swojej stronie.
Fot. www.tvp.info.pl
W danych uwzględniono pięć krajów, w tym Polskę. Na wykresie widać, że liczba aktywnych przypadków zakażenia zaczyna spadać w Niemczech, Hiszpanii, Francji i we Włoszech, natomiast w Polsce – cały czas rośnie. Problem pojawia się jednak przy bardziej szczegółowej analizie.
2 500 czy 25 000, czyli „mniejsza” i „większa” skala dla tego samego wykresu
Aby sprawdzić, ile dokładnie przypadków było aktywnych w poszczególnych krajach, trzeba spojrzeć na oś Y. Tyle że na osi po lewej stronie widzimy zupełnie inne wartości niż po prawej stronie. Liczby z prawej strony są dziesięciokrotnie większe (dodano jedno zero do każdej liczby), co całkowicie zaburza odbiór informacji zawartych na wykresie.
Efekt zastosowania „mniejszej” skali dla Polski i „większej” dla pozostałych krajów jest taki, że np. 17 maja zdaje się, jakby to w naszym kraju było najwięcej aktywnych zakażeń. A przecież jest inaczej: jeśli przyporządkuje się każde z państw do prawidłowej skali, okaże się, że tego dnia odnotowano w Polsce nieco ponad 10 tys. aktywnych zakażeń, a np. w Hiszpanii (która jest znacznie niżej na wykresie) – nieco ponad 50 tys.
W tym przypadku danych na wykresie jest więc z jednej strony za mało (nie wiadomo, które krzywe przedstawionych państw odnoszą się do poszczególnych skali), a z drugiej strony, panuje tu nadmierny chaos (podobieństwo obu osi wprowadza w błąd).
Co tu się odwykresowało?
Wpadki związane z przygotowywaniem wykresów i rycin zdarzają się również u samego źródła, czyli w nauce. Dobrym przykładem jest wykres opublikowany na łamach „Journal of Tsinghua University (Science and Technology)” w artykule pt. „Effect of human movement on a patient’s exhaled viral particle transmission: A numerical study”.
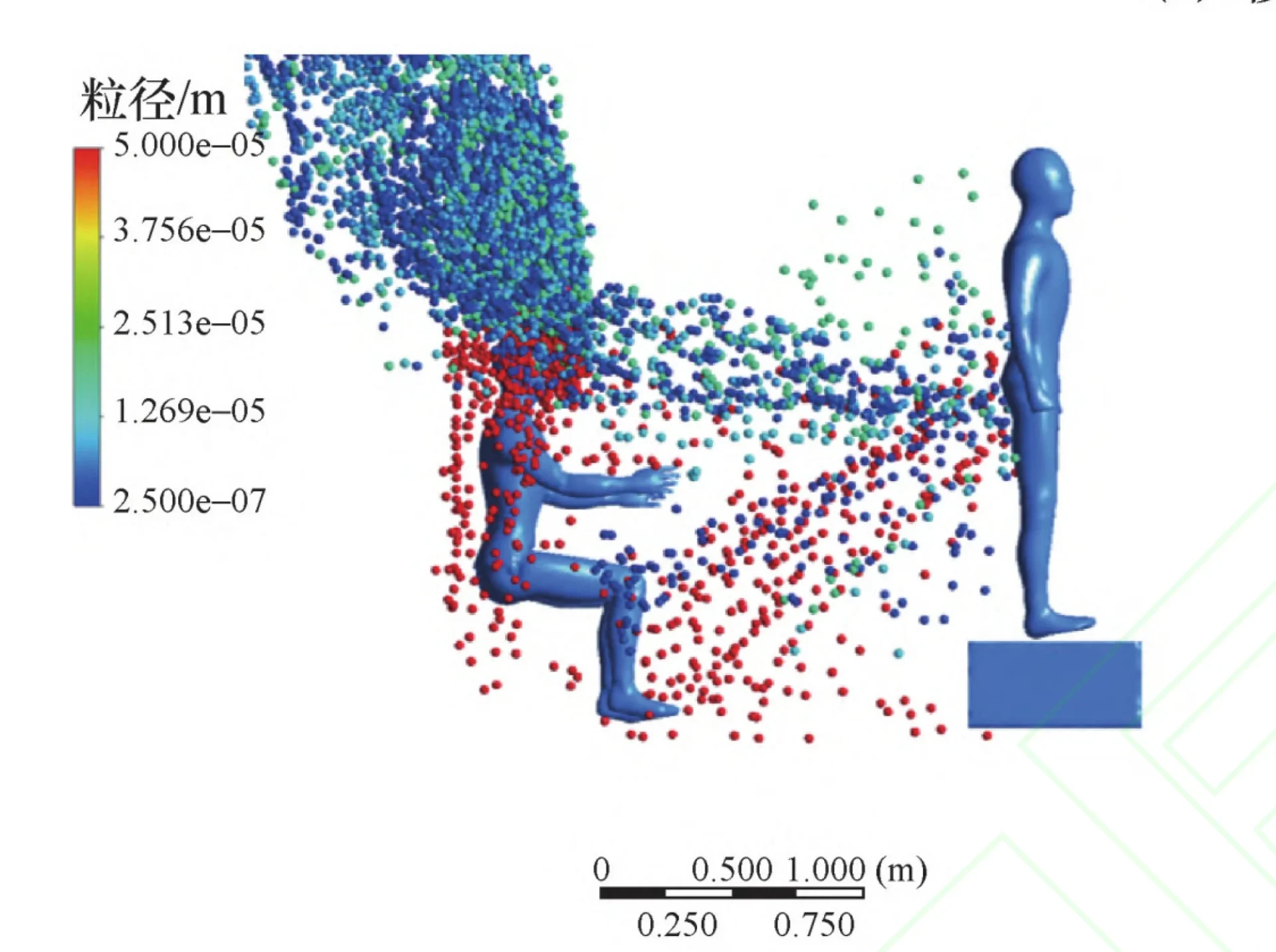
Fot. Jialin, W. U., Wenguo, W. E. N. G., & Ming, F. U. (2022). Effect of human movement on a patient’s exhaled viral particle transmission: A numerical study. Journal of Tsinghua University (Science and Technology), 62(6), 1044-1051.
Już na pierwszy rzut oka grafika wprawia w konsternację i prowadzi do pytań: Co w zasadzie ilustruje? Co robią ukazane na niej postaci? Jaki proces został tu uwidoczniony? Do czego odnosi się legenda po lewej stronie, a do czego ta u dołu ilustracji? Itd.
Takie pytania nie powinny się pojawiać w przypadku prawidłowo wykonanej grafiki. Ryciny i wykresy powinny przedstawiać dane w tak czytelny i uporządkowany sposób, by szybka analiza wizualna od razu dostarczała najważniejszych informacji.
Wykres, który trzeba objaśniać
Z lektury oryginalnej publikacji, w której zamieszczono powyższą rycinę, a także z artykułu medialnego, w którym opisano przytoczone badania i udzielono głosu jego autorom, wynika, że grafika dotyczy przemieszczania się cząstek koronawirusa.
Nawet gdy to wiemy, nadal nie możemy być pewni, co przedstawiono na ilustracji: Czy wiriony przemieszczają się od pośladków i pleców postaci po prawej stronie ku postaci po lewej stronie? Dlaczego jedna postać jest zwrócona tyłem do drugiej? Czemu jedna osoba siedzi z rękoma wyciągniętymi przed siebie, a druga – stoi?
Wnikliwa analiza omawianej publikacji oraz komentarzy do niej wskazuje, że celem badania zilustrowanego na grafice było określenie, w jaki sposób cząstki wydychanego powietrza (wraz z wirusami) przemieszczają się… w metrze. Postać po lewej stronie ma być więc pasażerem, który siedzi, a postać po prawej stronie to osoba, która stoi w środkowym korytarzu metra.
W rzeczy samej na wykresie to siedzący oddycha, a z jego dróg oddechowych wydobywają się cząstki o różnej wielkości (skalę rozmiaru ukazuje kolorowa legenda po lewej stronie). Im większe wydychane cząstki, tym większa jest ich masa, dlatego opadają one niżej (czerwone punkty na grafice). Im lżejsze, tym wyżej się wznoszą w przestrzeni wagonu (niebieskie punkty). Legenda na dole grafiki przedstawia natomiast odległość pomiędzy dwiema postaciami, przy czym jednostką skali jest metr.
Wzajemna weryfikacja wykresów – dobra metoda udoskonalania
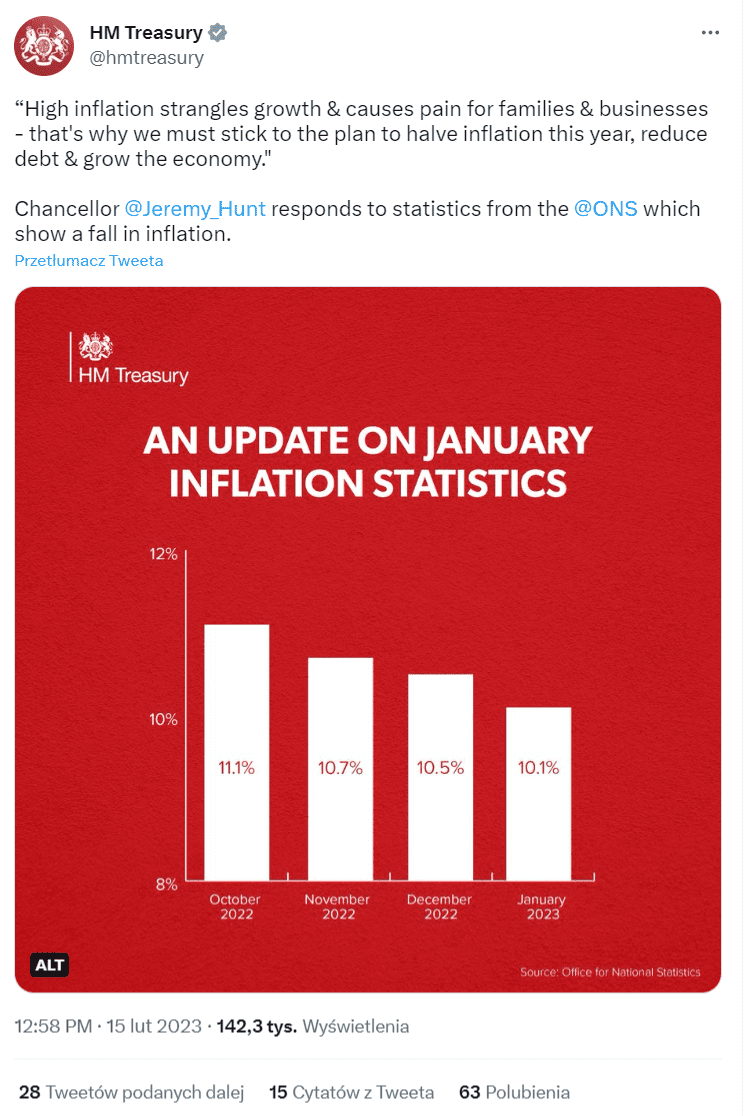
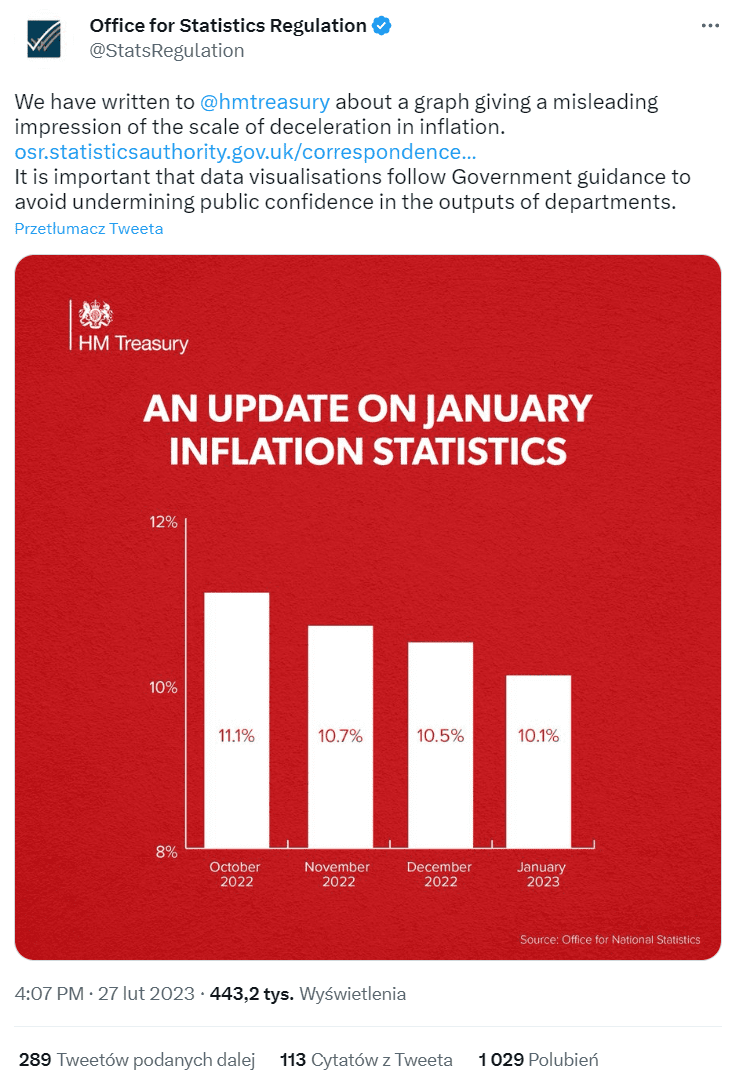
Na koniec warto podkreślić wagę dobrych praktyk oraz wzajemnej weryfikacji podmiotów udostępniających dane. Np. pod koniec lutego br. brytyjski Skarb Państwa Jego Królewskiej Mości opublikował na Twitterze wykres, który miał ukazać, że inflacja w państwie szybko spada.
Fot. Twitter
Jak widać, popełniono tu klasyczny błąd: oś Y rozpoczyna się nie od wartości 0 (zero), lecz od 8 proc., co sprawia, że prezentowany spadek inflacji zdaje się bardzo dynamiczny. Na tę nieprawidłowość szybko zareagował brytyjski Urząd ds. Regulacji Statystycznych, który odpowiedział własnym tweetem:
Fot. Twitter
W treści tweeta podano: „napisaliśmy do @HmTeasury w sprawie wykresu, który wprowadza w błąd, dając mylne wrażenie, dotyczące skali spadku inflacji. […] Przestrzeganie rządowych wytycznych w wizualizacjach danych jest bardzo istotne i pozwala uniknąć podważania zaufania publicznego do wyników udostępnianych przez departamenty”.
Warto rozwijać takie praktyki, w ramach których oficjalne podmioty, które powinny cieszyć się zaufaniem publicznym, wzajemnie się weryfikują i poprawiają, gdy dojdzie do błędu lub gdy interpretacja wykresu sprawia widoczne trudności odbiorcom.
Na co zwracać uwagę podczas analizy wykresu?
Możliwych nieprawidłowości na wykresach jest oczywiście znacznie więcej, niż przedstawiliśmy w tej analizie. Jednak wychwycenie tych błędów, na które zwróciliśmy uwagę, będzie dobrym początkiem – a takich przykładów w sieci znajdziemy wiele.
Jakie cechy wykresu powinny wzbudzić twoje wątpliwości:
- wykres ma „chwytliwy” tytuł, który nie opisuje tego, co widać na grafice, lecz stawia tezę,
- na grafice nie przedstawiono źródeł informacji,
- na wykresie nie widać osi Y lub oś Y przedstawia wartość inną niż 0 (zero),
- wykres porównuje zestawy danych, z których każdy ma inną skalę,
- na wykresie porównano dane, których nie da się ze sobą poprawnie porównać,
- wykres jest zbyt uproszczony (niepodpisane osie, niepodpisane krzywe lub słupki, nie wiadomo, które wartości reprezentują które zmienne),
- na wykresie wykorzystano jaskrawe kolory według nieuzasadnionego klucza (tylko po to, by potwierdzić stawianą tezę),
- na wykresie panuje nadmierny chaos, nie wiadomo, do czego odnoszą się poszczególne dane itp.
Dowiedz się, jak radzić sobie z dezinformacją w sieci
Poznaj przydatne narzędzia na naszej platformie edukacyjnej
Sprawdź!
*Jeśli znajdziesz błąd, zaznacz go i wciśnij Ctrl + Enter
POLECANE DLA CIEBIE
